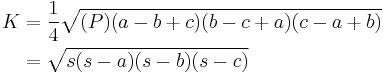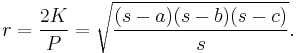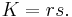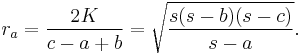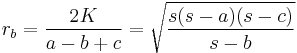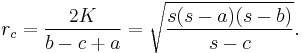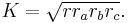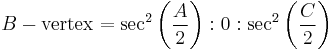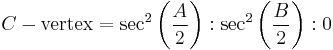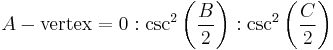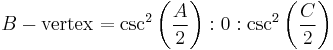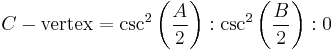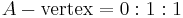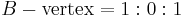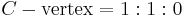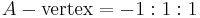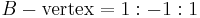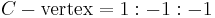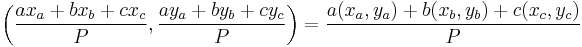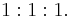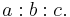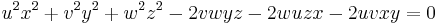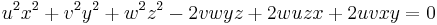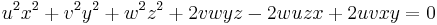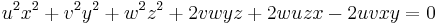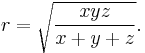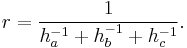Incircle and excircles of a triangle

In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is called the triangle's incenter.

An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides.

The center of the incircle can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle and the external bisectors of the other two. Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form an orthocentric system.

See also Tangent lines to circles.

Contents

Relation to area of the triangle

The radii of the in- and excircles are closely related to the area of the triangle. Let K be the triangle's area and let a, b and c, be the lengths of its sides. By Heron's formula, the area of the triangle is

\begin{align} K & {} = \frac{1}{4}\sqrt{(P)(a-b%2Bc)(b-c%2Ba)(c-a%2Bb)} \\ & {} = \sqrt{s(s-a)(s-b)(s-c)} \end{align}

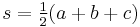where s= \tfrac{1}{2}(a%2Bb%2Bc) is the semiperimeter and P = 2s is the perimeter.

The radius of the incircle (also known as the inradius, r ) is

r = \frac{2K}{P} = \sqrt{\frac{(s-a)(s-b)(s-c)}{s}}.

Thus, the area K of a triangle may be found by multiplying the inradius by the semiperimeter:

\displaystyle K=rs.

The radii in the excircles are called the exradii. The excircle at side a has radius

r_a = \frac{2K}{c-a%2Bb} = \sqrt{\frac{s (s-b)(s-c)}{s-a}}.

Similarly the radii of the excircles at sides b and c are respectively

r_b = \frac{2K}{a-b%2Bc} = \sqrt{\frac{s (s-a)(s-c)}{s-b}}

and

r_c = \frac{2K}{b-c%2Ba} = \sqrt{\frac{s (s-a)(s-b)}{s-c}}.

From these formulas one can see that the excircles are always larger than the incircle and that the largest excircle is the one tangent to the longest side and the smallest excircle is tangent to the shortest side. Further, combining these formulas with Heron's area formula yields the result that[1]:#4

K=\sqrt{rr_ar_br_c}.

Nine-point circle and Feuerbach point

The circle tangent to all three of the excircles as well as the incircle is known as the nine-point circle. The point where the nine-point circle touches the incircle is known as the Feuerbach point.

Gergonne triangle and point

The Gergonne triangle of ABC is denoted by the vertices TA, TB and TC that are the three points where the incircle touches the reference triangle ABC and where TA is opposite of A, etc. This triangle TATBTC is also known as the contact triangle or intouch triangle of ABC. The incircle of ABC is the circumcircle of TATBTC. The three lines ATA, BTB and CTC intersect in a single point, the triangle's Gergonne point Ge - X(7). Interestingly, the Gergonne point of a triangle is the symmedian point of its Gergonne triangle. For a full set of properties of the Gergonne point see.[2]

The touchpoints of the excircle with segments BC,CA,AB are the vertices of the extouch triangle. The points of intersection of the interior angle bisectors of ABC with the segments BC,CA,AB are the vertices of the incentral triangle.

Nagel triangle and point

The Nagel triangle of ABC is denoted by the vertices XA, XB and XC that are the three points where the excircles touches the reference triangle ABC and where XA is opposite of A, etc. This triangle XAXBXC is also known as the extouch triangle of ABC. The circumcircle of the extouch triangle XAXBXC is called the Mandart circle. The three lines AXA, BXB and CXC intersect in a single point, the triangle's Nagel point Na - X(8).

Trilinear coordinates for the vertices of the intouch triangle are given by

Trilinear coordinates for the vertices of the extouch triangle are given by

Trilinear coordinates for the vertices of the incentral triangle are given by

Trilinear coordinates for the vertices of the excentral triangle are given by

Trilinear coordinates for the Gergonne point are given by

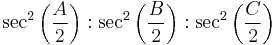\sec^2\left(\frac{A}{2}\right)�: \sec^2 \left(\frac{B}{2}\right)�: \sec^2\left(\frac{C}{2}\right),

or, equivalently, by the Law of Sines,

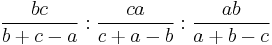\frac{bc}{b%2B c - a}�: \frac{ca}{c %2B a-b}�: \frac{ab}{a%2Bb-c}.

Trilinear coordinates for the Nagel point are given by

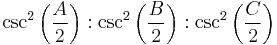\csc^2\left(\frac{A}{2}\right)�: \csc^2 \left(\frac{B}{2}\right)�: \csc^2\left(\frac{C}{2}\right),

or, equivalently, by the Law of Sines,

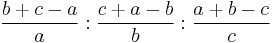\frac{b%2B c - a}{a}�: \frac{c %2B a-b}{b}�: \frac{a%2Bb-c}{c}.

It is the isotomic conjugate of the Gergonne point.

Coordinates of the incenter

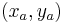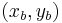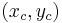The Cartesian coordinates of the incenter are a weighted average of the coordinates of the three vertices using the side lengths of the triangle as weights. (The weights are positive so the incenter lies inside the triangle as stated above.) If the three vertices are located at (x_a,y_a), (x_b,y_b), and (x_c,y_c), and the sides opposite these vertices have corresponding lengths a, b, and c, then the incenter is at

\bigg(\frac{a x_a%2Bb x_b%2Bc x_c}{P},\frac{a y_a%2Bb y_b%2Bc y_c}{P}\bigg) = \frac{a(x_a,y_a)%2Bb(x_b,y_b)%2Bc(x_c,y_c)}{P}

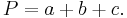
where \ P = a %2B b %2B c.

\ 1�: 1�: 1.
\ a�: b�: c.

Equations for four circles

Let x : y : z be a variable point in trilinear coordinates, and let u = cos2(A/2), v = cos2(B/2), w = cos2(C/2). The four circles described above are given by these equations:

  • Incircle:
\ u^2x^2%2Bv^2y^2%2Bw^2z^2-2vwyz-2wuzx-2uvxy=0
  • A-excircle:
\ u^2x^2%2Bv^2y^2%2Bw^2z^2-2vwyz%2B2wuzx%2B2uvxy=0
  • B-excircle:
\ u^2x^2%2Bv^2y^2%2Bw^2z^2%2B2vwyz-2wuzx%2B2uvxy=0
  • C-excircle:
\ u^2x^2%2Bv^2y^2%2Bw^2z^2%2B2vwyz%2B2wuzx-2uvxy=0

Other incircle properties

Suppose the tangency points of the incircle divide the sides into lengths of x and y, y and z, and z and x. Then the incircle has the radius[3]

r = \sqrt{\frac{xyz}{x%2By%2Bz}}.

If the altitudes from sides of lengths a, b, and c are ha, hb, and hc then the inradius r is one-third of the harmonic mean of these altitudes, i.e.

r = \frac{1}{h_a^{-1}%2Bh_b^{-1}%2Bh_c^{-1}}.

The distance between the circumcenter and the incenter is 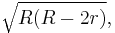\sqrt{R(R-2r)}, where r is the incircle radius and R is the circumcircle radius.[4] Thus the incircle radius is no larger than half the circumcircle radius (Euler's triangle inequality).[4]

The product of the incircle radius and the circumcircle radius of a triangle with sides a, b, and c is[5] 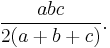\frac{abc}{2(a%2Bb%2Bc)}.

Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter (the center of its incircle). There are either one, two, or three of these for any given triangle.[6]

See also

References

  1. ^ Baker, Marcus, "A collection of formulae for the area of a plane triangle," Annals of Mathematics, part 1 in vol. 1(6), January 1885, 134-138. (See also part 2 in vol. 2(1), September 1885, 11-18.)
  2. ^ Dekov, Deko (2009). "Computer-generated Mathematics : The Gergonne Point". Journal of Computer-generated Euclidean Geometry 1: 1–14.. http://www.dekovsoft.com/j/2009/01/JCGEG200901.pdf. 
  3. ^ Chu, Thomas, The Pentagon, Spring 2005, p. 45, problem 584.
  4. ^ a b Nelson, Roger, "Euler's triangle inequality via proof without words," Mathematics Magazine 81(1), February 2008, 58-61.
  5. ^ Johnson, Roger A., Advanced Euclidean Geometry, Dover, 2007 (orig. 1929), p. 189, #298(d).
  6. ^ Kodokostas, Dimitrios, "Triangle Equalizers," Mathematics Magazine 83, April 2010, pp. 141-146.

External links

Interactive